|
Building
the Digital Representation
|
This example from Volume 8 of The
Writings of Charles S. Peirce illustrates major steps
in the editing and production process and exhibits the master
files that are involved. The selection titled “Logical
Studies of the Theory of Numbers,” not previously
published, builds upon earlier work of Peirce, especially
the system he published in American Journal of Mathematics
in 1881 as “On the Logic of Number.” The first
two of the four pages of the copy-text appear here and provide
the text for the transcription and editing samples that
follow.
|
|
 |
|
1
Transcription and transcription notes
are shown here in a view suitable for proofreading and correcting.
The two files are visually linked by tags of the form {TRN #}.
The characters “1:” in the transcription notes indicate
that a note is linked to text on p. 1. The page number is
automatically generated; a line number will be added in final
layout.
The bottom frame shows the blue-highlighted
sample from the SGML master file that contains a logical expression
whose tagging is patterned after the XML/MathML standard. (Mathematics
operators in <mo> are controlled in their symbols and spacing
by the template and automatically filled in.) After this expression,
the last on the manuscript page, is a pagebreak marker, <pagebreak>,
and information within it about the numbering (in this case based
on the microfilm serial numbering).
FrameMaker software automates much of the keyboarding
of elements and their attributes and also maintains links or cross
references between files.
|
| |
| |
|
Logical Studies of the Theory of Numbers.
The object of the present investigation
is to analyze carefully the logic of the theory of numbers.
I especially desire to clear up the question of whether
there can be fundamentally different ways of proving {TRN
1}a{\TRN 1} theorem from given premises; and the law of
reciprocity seems likely to be instructive in this respect.
I also wish to know whether there is not a regular method
of proof {TRN 2}in{\TRN 2} the higher arithmetic, so that
{TRN 3}we{\TRN 3} can see in advance precisely how a given
proposition is to be demonstrated.
I make use of my last notation for relatives.
I {TRN 4}write{\TRN 4} {TRN 5} li {\TRN 5} to
mean that
……………………
write {TRN 19} lij {\TRN 19}
to signify that {TRN 20}l{\TRN 20}, {TRN 21}i{\TRN 21} and
{TRN 22}j{\TRN 22} are connected; thus, {TRN 23}l{\TRN 23}
might be a mode of relation; and {TRN 23}i{\TRN 23} and
{TRN 24}j{\TRN 24} two objects so related the one to the
other.
I use the signs of addition and multiplication
{TRN 25}as{\TRN 25} in the modified Boolian calculus. Thus,
{TRN 26} li mj {\TRN 26} {TRN 27}means{\TRN
27} that {TRN 28}l{\TRN 28} and {TRN 29}i{\TRN 29} are connected
and also {TRN 30}m{\TRN 30} and {TRN 31}j{\TRN 31}.
While {TRN 32} li + mj {\TRN 32} means
that either {TRN 33}l{\TRN 33} and {TRN 34}i{\TRN
34} are connected or else {TRN 35}m{\TRN 35} and {TRN 36}j{\TRN
36}.
|
|
|
|
6.8.xd “Logical Studies of the Theory of Numbers”
NOTES file
Transcription Notes
TRN 1 1: a] bef del prop
TRN 2 1: in] i ov o
TRN 3 1: we] ov illeg
TRN 4 1: write] wri ov desi
TRN 5 1: li] mark ital
…………………….
TRN 19 1: lij] mark ital
TRN 20 1: l] mark ital
TRN 21 1: i] mark ital
TRN 22 1: j] mark ital
TRN 23 1: i] mark ital
TRN 24 1: j] mark ital
TRN 25 1: as] ms page torn so as to
obscure word
TRN 26 1: li mj]
letters mark ital
TRN 27 1: means] ms page torn so as
to obscure word
TRN 28 1: l] mark ital
TRN 29 1: i] mark ital
TRN 30 1: m] mark ital
TRN 31 1: j] mark ital
TRN 32 1: li + mj]
first three letters mark ital; ms torn after the m and
the dot on conjectured subscript j which are still visible
on archival ms
TRN 33 1: l] mark ital
TRN 34 1: i] mark ital
TRN 35 1: m] mark ital
TRN 36 1: j] mark ital
|
|
|
|
|
| |
|
|
|
|
| |
|
<writingsvol><volume><body><sel
status = "transcription"><headingrun text
= "Logical Studies of the Theory of Numbers"><heading>Logical
Studies of the Theory of Numbers</heading>
………..
While <notelinkbeg
dref = "1023743" id = "1115954" format
= "NoteLinkBeg">
<logic><mi
role = "var">l</mi><msub><mi
role = "var">i</mi></msub>
<mo token =
"plus" form = "infix"><ms></ms></mo>
<mi role =
"var">m</mi><msub><mi
role = "var">j</mi></msub>
</logic><notelinkend
dref = "1023743" format = "NoteLinkEnd"><pagebreak
text = "end of S4:2; no number on ms."> means
that either
|
|
|
|
|
| |
|
|
|
|
 |
|
|
|
|
|
2
Emended copy-text and textual apparatus
are prepared after the perfected transcription is archived. Transcription
notes are categorized as “alterations” (visually tagged
as ALT), “format indicators” (FOR), “line-end
hyphenations” (LEH), or “external to the text”
(EXT). The editors also introduce emendations (E), regularizations
(REG), and rejected substantives (REJ), as well as select alterations
for the print edition (SA). Textual notes (TN) will be illustrated
later with the headnote.
Additional properties are identified, such
as Peirce’s highlighting which is marked by the <hi>
element (see the SGML frame lower left). Font and format are governed
by elements and their attributes.
|
| |
|
|
|
|
| |
|
{REG 1}Logical Studies of the Theory of
{E 1}Numbers{\E 1}{\REG 1}
………..
there is not a regular method of proof
{ALT 2}in{\ALT 2} the higher arithmetic, so that {ALT 3}we{\ALT
3} can see in advance precisely how a given proposition
is to be demonstrated.
I make use of my last notation for relatives.
I {ALT 4}{SA 1}write{\SA 1}{\ALT 4} {FOR 1} li
{\FOR 1} to mean that two objects {FOR 2}l{\FOR 2}
and {FOR 3}i{\FOR 3} are connected. These two objects
generally pertain to different universes; thus, {FOR 4}l
{\FOR 4}may be a {FOR 5}character{\FOR
5} and {FOR 6}i{\FOR 6} a {FOR 7}thing.{\FOR
7} But there is no reason why I should {ALT 5}not,{\ALT
5} instead of {FOR 8} li {\FOR 8}, write
{FOR 9}(l,i){\FOR 9}, except that the first
way is more compact. A line over an {LEH 1}expression{\LEH
1} negatives it, so that {FOR 10}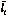 {\FOR 10} means
that {FOR 11}l{\FOR 11} and {FOR 12}i{\FOR
12} are disconnected. I also
………..
I use the signs of addition and multiplication
{EXT1}as{\EXT1} in the modified Boolian calculus. Thus,
{FOR 19} li mj
{\FOR 19} {EXT2}means{\EXT2} that {FOR 20}l{\FOR
20} and {FOR 21}i{\FOR 21} are connected and also
{FOR 22}m{\FOR 22} and {FOR 23}j{\FOR 23}.
While {EXT3}{TN 1}{FOR 24} li + mj
{\FOR 24}{\TN 1}{\EXT3} means that either {FOR 25}l{\FOR
25} and {FOR 26}i{\FOR 26} are connected or else
{FOR 27}m{\FOR 27} and {FOR 28}j{\FOR 28}.
I further use the symbols S
and P as follows. {FOR 29}Si
{\FOR 29}means that {FOR 30}i {\FOR 30}is {ALT 6}{SA
2}something{\SA 2}{\ALT 6} suitably selected from the universe
of {FOR 31}i’s{\FOR 30}, while {FOR 32}Pi
{\FOR 32}means that {FOR 33}i
|
|
|
|
6.8.xd “Logical Studies of the Theory
of Numbers” NOTES file
Alterations
………..
ALT 2 1: in] i ov o
ALT 3 1: we] ov illeg
ALT 4 1: write] wri ov desi
ALT 5 1: not,] comma add; bef del
write,
ALT 6 1: something] intl ab del anything
ALT 7 1: may] m ov is
………..
Format
FOR 1 1: li] mark ital
FOR 2 1: l] mark ital
FOR 3 1: i] mark ital
FOR 4 1: l ] mark ital
FOR 5 1: character] mark ital
FOR 6 1: i] mark ital
………..
Line-End Hyphenation
LEH 1 1: expression] ex-\pression
………..
Extra Textual
EXT 1 1: as] ms page torn so as to obscure
word
EXT 2 1: means] ms page torn so as to
obscure word
EXT 3 1: li + mj]
ms torn after the m and the dot on conjectured subscript
j which are still visible on archival ms
Regularizations
REG 1 1: Logical Studies of the Theory
of Numbers] in ms is ab short centered horizontal line
………..
Emendations
E 1 1: Numbers] E; ~.
E 2 3: lij] E;
lij
………..
Selected Alterations
SA 1 1: write] desi[gnate]
SA 2 3: something] anything
SA 3 3: may be] is
|
|
|
| |
|
|
|
|
| |
|
may be a
<notelinkbeg
dref = "1023497" id =
"1115604"
format = "NoteLinkBeg">
<hi rend =
"italic">character</hi>
<notelinkend
dref = "1023497" format =
"NoteLinkEnd">
and
|
|
|
|
|
|
|
|
|
|
|
3
Steps towards page layout begin when copy-text
is emended. The selection number “1” at the top of
the page will be automatically replaced by the appropriate sequential
number when the selection is placed within the volume file. All
references to this selection elsewhere in the volume will be automatically
updated at that point.
Throughout the production process each of the
visual tags, such as {ALT 1}, is a hyperlink taking an editor
to the relevant textual apparatus note.
Information for content annotations is collected
in the annotations file, illustrated on the right. This
textual (SGML) database preserves in one place all of the working
notes by editors and consultants that go into the historical research
for the annotations. It also contains the final, published annotations.
The frame at the bottom illustrates the SGML structure of the
annotations file.
|
| |
| |
|
|
| |
|
<anngroup><link id = "1241638">W8.xd.1.4–5</link><phrase>law
of reciprocity</phrase>
<annotation type = "printver1.0"
resp = "adt"><p>The law of quadratic
reciprocity was first
… </annotation>
<annotation type = "draft"
resp = "adt"><p>http://www.math.umn.edu/~wittman/problems2.html:
the
… </annotation></anngroup>
…
<anngroup status = "retired"><link
id = "1041370">W8.xd.2.12–13</link><phrase>I
use the
signs of addition and multiplication as
in the Boolian calculus.</phrase>
<annotation type = "draft"
resp = "de waal"><p>CROSS REFERENCE
W8.za.1.11a </p></annotation>
<annotation type = "draft"
resp = "adt"><p>ADT: No need for
this cross-reference.</p>
</annotation></anngroup>
|
|
|
|
4
As the selection page layout for the
print edition is perfected, the visual tags are hidden and the
textual apparatus is put in next-to-final form. In the
textual notes, temporary numbering (such as “E 1”)
will be dropped and line numbers inserted after the page numbers.
The call-out box illustrates the SGML structure
of the apparatus file. <EdInsert> encloses editorial insertions;
italic square brackets are automatically added.
|
|
5
These examples conclude with two of the most
important components that form the background for all of the preceding
steps. On the left is the start of the <TEIHeader>
element for the sample selection. This element is included at
the beginning of every file and contains basic metadata about
the file including a record of all changes to it. It documents
the various editorial stages giving dates and editors responsible.
On the right is a section from FrameMaker’s
Element Definition Document (EDD). The <Heading>
element is typical in that it begins with the basic description
imported from the SGML Document Type Definition followed by format
rules specific to the FrameMaker application. It indicates, for
example, that if a heading is the first one under a major frontbody
division then it will be in 18-point font size. The EDD thus provides,
in effect, specifications for the layout of the print edition.
(Clicking on its image opens up a PDF version of the complete
document.)
|
|
 |
![Text Box: <tnotegroup type = "tn"><heading>Textual Notes</heading>
<tnote id = "1033823"><pagelineref><pageref dref = "1119081"></pagelineref>by <math>
<mi role = "var">l</mi></math>.] The continuous text of RS 4:2 and R 36:17 ends here at mid-page. Leaves R 36: 16 and 18 appear to continue the discussion without a discernable break in content.</tnote></tnotegroup>
<tnotegroup type = "e"><heading>Emendations</heading>
<tnote id = "1023253"><pagelineref><pageref dref = "1117435"></pagelineref>Numbers]E; ~. </tnote> …
<tnotegroup type = "sa"><heading>Selected Alterations</heading>
<tnote id = "1023464"><pagelineref><pageref dref = "1117772"></pagelineref>write] desi<EdInsert> gnate</EdInsert></tnote>](digital_files/image024.gif)
