Preliminary Sketch of Logic

MS 154: Fall 1869


§1. Logic is the science needed in order to test arguments.

The science required for any testing is one which merely divides its object into its natural kinds and describes the characters of each kind. Thus a "Bank-Note Detector" affords the knowledge requisite to testing bank-notes and it describes each kind of bank-note merely, without entering into an account of its manufacture. Such a knowledge will be termed a classificatory in opposition to a causal or demonstrative science.

§2. An argument is a statement supposed to appeal to some person. Appealing is having such a relation to a person that he will regard the statement as if he would admit that every set of facts, taken as those stated have been taken, determines by certain relations another possible statement, and that this would be more apt to be true in the long run when the facts stated are true, than a random assertion would be. 1

That which is laid down is termed the premiss or premises; the determinate proposition to which the premise or premises are related is termed the conclusion; and the implication that such a conclusion is usually true if the premises are is termed the leading principle.

§3. A valid argument (opposed to a fallacious argument or fallacy) is one whose leading principle is true.

A demonstrative (opposed to a merely probable) argument is one whose leading principle would make every such conclusion true and not merely the greater number of them.

§4. An argument determines its conclusion to be true, only if both leading principle and premisses are true. Whatever is required besides the premises to determine the truth of the conclusion is ipso facto implied in the leading principle. Hence whatever fact (not superfluous) is dropped from the premises is added to the leading principle; and no fact can be eliminated from the leading principle without having been added to the premises. All that is in the premisses cannot however be thrown into the leading principle, since there is no argument which states nothing. Nor is there an argument without a leading principle, for if nothing is implied the conclusion is already stated in the premisses. But a mere statement is not an argument.

§5. That there is a certain minimum leading principle, that cannot be got rid of may be illustrated as follows. Let a certain argument be A and its conclusion, B. Then we may say that the leading principle is that "If A is true B is true." Take this as an additional premiss and the argument becomes--

 
If A, B
But A
Ergo B.

 

The leading principle of this plainly is that if two facts are related as reason and consequent and the reason be true the consequent is true. Make another premise of this and the argument becomes--

If one statement be related to another so that if the former is true the latter is and if the former is true, the latter is.

A is so related to B and is true
Ergo B is true.

Now the leading principle of this is plainly the same as that of the last previous form of the argument. Here, therefore, is a leading principle which is not dispensed with by being thrown into the premiss. And as it is absurd to say that anything can be eliminated from the leading principle by taking away anything from the premises, it is plain this principle must have lurked in the leading principle even of the first form of the argument.

An argument in which everything has been eliminated from the leading principle which can be so eliminated is termed a complete in opposition to an incomplete or rhetorical argument or enthymeme. 2

Logic is, of course, not the encyclopaedia. Those things which can possibly be required to be stated have as such no truth in common and are in detail the object of the various sciences. Hence logic does not take account of the truth of premisses, or of anything which would appear as a premiss if the argument were put into the complete form. On the other hand whatever cannot be eliminated from the leading principle is taken for granted by every other science and not laid down; hence logic does take account of these things. Logic might, indeed, be defined as the science of the leading principles of complete arguments; and such leading principles are properly termed logical principles.

The example of a logical principle given above illustrates an important character of all such principles; namely, that they not only cannot be stated in arguments without superfluity but that in one sense they cannot be stated at all. The statement which contains only a logical principle contains no fact. In order to infer so as to conform to logical principles we must infer a determinate conclusion, but in order to state what shall imply a logical principle we are not obliged to make any definite statement at all.

§6. A proposition is a collocation of significant terms so put as to state something.

To state is to purport to represent an object--or in other words, to represent that whatever a certain significant term represents is represented by another significant term.

The manner in which the significant terms are put together--or the sign that they are so put together--is termed the copula. This is essentially the same for all propositions.

The term whose object is said to be represented by another may be called the true subject; that which is said to represent the object of the other may be called the true predicate.

§7. A significant term is something which stands for an object, by means of its relation to a certain symbol or symbols.

A symbol is something to which a certain character is imputed, that is which stands for whatever object may have that character.

§8. Mere iteration is not argument, for it could not appeal to any mind that did not admit the fact asserted, and one that already admitted it it would not affect. In short, it does not fall strictly under the definition of argument nor is it analogous to it. Every conclusion therefore states something different from any one of its premisses. But the copula is the same for all propositions. Hence the conclusion must be obtained from any premiss by the substitution of a significant term or terms.

That another significant term or terms may be substituted for a term or terms of a premise, requires to be put into another premise in a complete argument, unless the substitution is wholly determined by a principle implied by every such argumentative substitution. But in this case the principle would be implied in the very premiss itself and therefore the conclusion would merely repeat a part of what is implied in the premise, which we have just seen is impossible. In all cases, therefore, a second premiss is required to express the condition which makes it possible to substitute the conclusion for the first premise.

If more premisses than one are required to express the fact that the conclusion can be substituted for any given premise, either these other premisses by themselves yield one conclusion which expresses this fact or successive substitutions can be made by single propositions. Hence every argument of more than two premisses can be broken up into arguments of two premisses. Such arguments are called simple arguments in opposition to complex ones.

§9. The substitution of conclusion for a premiss is as we have seen the substitution of one term for another.

Now, it is evident that the only such substitution which necessarily yields a true conclusion from true premises is the substitution for a subject or predicate of another term which has as subject or predicate no function or value beyond that of the term for which it is substituted.

We thus get such an argument as this--
S has no force as subject beyond M
P has no force as predicate beyond M
S is P

or in other language
S is denoted by M
M connotes P
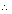S is P

 

This principle is that of deduction.

§10. Passing over for the present the divisions of mood and figure, also over the question whether there is any other form of predication except that in which the predicate is said to denote and to be connoted by the subject, we come to another principle of inference.

1. This sufficiently sets forth the essential elements of an argument; but does not define it, since in introducing the conception of truth it commits a diallele.

2. Aristotle makes the rhetorical argument the same as the probable one. This is an error.